|
Цели
Показать, что
лист Мёбиуса - объект топологии.
Сформулировать свойства листа Мёбиуса,
Рассмотреть
применение листа Мёбиуса на практике
Задачи
Расширение и
углубление знаний по математике
Привитие
интереса к предмету.
Формирование
научно-исследовательских навыков.
Формирование
навыков самостоятельной работы.
Формирование навыков работы в группе.
Постановка проблемы
исследования :
Как то на уроке в 6в классе мы изучали
рациональные числа и выясняли , что их бесконечно много.
Тогда мы заговорили о символе бесконечности в математике.
Всем стало интересно откуда взялся этот символ ,
интересовала история его появления и что самое интересное
какая же геометрическая фигура может ему соответствовать!
Тогда то учитель нам и рассказал что
символом бесконечности служит лист Мебиуса , что это
одновременно простая и загадочная фигура , исследования
листа Мебиуса идут с 19 века до наших времен!
Самое интересное , что изготовить лист
Мебиуса может каждый с помощью бумаги, ножниц и клея!
А когда прямо на уроке учитель нам
показал несколько фокусов с листом Мебиуса, то мы решили
подробнее исследовать это тело. Тем более что опрос
родителей, одноклассников и старшеклассников показал : как
ничтожно мало людей знают про лист Мебиуса!
Введение
Геометрия-слово греческое, в переводе на
русский язык означает землемерие, изучает свойства фигур.
Как и любая наука геометрия делится на разделы
I Планиметрия
(лат. слово, планум - поверхность, плоскость + метрия),
раздел геометрии, изучающий свойства фигур на плоскости
(треугольник, квадрат, круг, окружность и т.д.)
2.Стереометрия (греч, стереос -
пространство + метрия), раздел геометрии, изучающий свойства
фигур в пространстве (шар, куб, параллелепипед и т.д.)
З.Топология (гр. топос - место, местность + логия) является
одним из самых
«молодых» разделов современной
геометрии, в котором изучаются свойства
таких фигур, которые не изменяются при
деформациях (растяжение, сжатие), не допускающих разрывов и
склеивания.
Родоначальниками топологии были немецкий
учёный Георг Кантор (1845-1918), Феликс Хаусдорф, Павел
Сергеевич Александров (1896-1982).
Топология
Как было
сказано выше, что топология изучает свойства таких фигур,
которые не изменяются при деформациях, не допускающих
разрывов и склеивания. С точки зрения топологии баранка и
кружка одно и тоже. Сжимая и растягивая кусок резины можно
перейти от одной из этих фигур к другой. А вот баранка и шар
- разные объекты; чтобы сделать отверстие, надо разорвать
баранку. Примерами топологических фигур могут быть фигуры:
Среди букв
русского алфавита есть топологически одинаковые фигуры А-Д,
Г-С, С-П, Л-И, 3-Э, Т-У.
Примеры не
равных фигур в топологии:
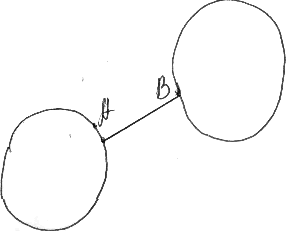
Вторая фигура
получается из первой путем склеивания точек С 1
и Д 1, С 2 и Д 2 и
растяжения отрезка АВ. Топологические равенства отличаются
от равенств в геометрии твёрдых фигур, где равенство фигур
равносильна равенству измерении. В топологии фигуры не
имеют измерений.
Самым
известным объектом в топологии является лист Мёбиуса.
Историческая
справка
Таинственный
и знаменитый лист Мёбиуса придумал в 1858 году немецкий
геометр
Август Фернанд Мебиус (1790 - 1868), ученик «короля
математиков» Гаусса. Мёбиус был первоначально астрономом,
как Гаусс и многие другие из тех, кому математика обязана
своим развитием. В те времена занятия математикой не
встречали поддержки, а астрономия давала достаточно денег,
чтобы не думать о них, и оставляло время для собственных
размышлений. И Мёбиус стал одни из крупнейших геометров
XIX
века. В возрасте 68 лет ему удалось сделать открытие
поразительной красоты. Идея пришла ему в голову, когда
служанка не правильно сшила ленту. Мебиус родился в
Шульпфорте. Некоторое время под руководством К. Гаусса
изучал астрономию. С 1816г. Начал вести самостоятельные
астрономические наблюдения в Плейсенбургской обсерватории ,
в 1818г. Стал ее директором , позже- профессором
Лейпцигского университета. |